Wednesday, 27 February 2013
Superposition theorem
Do you like this story?
Superposition theorem
The Superposition theorem states that if a linear system is driven by more
than one independent power source, the total response is the sum of the
individual responses.
If the network contains more than one voltage or current source, superposition allows for a solution to be found by considering each voltage or current source separately and then adding the results. To consider each source separately, all other voltage sources are open circuited and all other current sources are short circuited.
If the network contains more than one voltage or current source, superposition allows for a solution to be found by considering each voltage or current source separately and then adding the results. To consider each source separately, all other voltage sources are open circuited and all other current sources are short circuited.
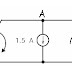
EXAMPLE
Find Vx
Solution
Consider 4V source
From the above circuit
resistors 2Ω and 5Ω are in parallel
Resultant resistance is =
( 2 * 5 ) / (2 + 5) = 10 / 7
Replacing the resultant
resistance in the given circuit
Adding 3Ω and 10/7 Ω we
get 31/7 Ω
Applying voltage divider
rule Vx = V * ( R1/ (R1 + R2 ) we get
Vx = 4 * ( 7 / 38 ) = 28/38 = 0.7368 V
Vx = 0.7368 V
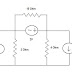
Now considering 5V source
Rearranging the above
circuit
Applying nodal analysis at
node A
Assume node voltage be Va
Va + Va + Va
– 5 = 0
4 5 2
4 5 2
Solving above equation we
get Va = (50 / 19 ) V
Applying voltage division
rule
Voltage across 1 Ω
resistance = 0.6578 V
If we compare above
circuit with given circuit the polarities are opposite to each other.So reverse the sign of
voltage across 1 Ω
Therefore Voltage across 1
Ω resistance Vx = ─ 0.6578 V
Now consider 2A current source
From the above circuit 2 Ω
and 5 Ω are in parallel
So resultant resistance =
(10 / 7) Ω
(10 / 7) Ω and 1Ω are in
series then the resultant circuit = ( 17
/ 7 ) Ω
Applying current division
rule
Current through desired
resistance = (current * opposite resistance ) total resistance
Current through ( 17 / 7 )
Ω resistance = 1.105 A
If we expand ( 17 / 7 ) Ω resistance,
we get
Vx = 1* 1.105 = 1.105 V
Vx = 1.105 V
Therefore by superposition theorem voltage across 1
Ω resistance is
Vx = 0.7368 ─ 0.6578
V + 1.105
Vx = 1.184 V

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter
Subscribe to:
Post Comments (Atom)













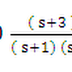





4 Responses to “Superposition theorem”
26 October 2014 at 15:31
sorry but i think you mean all voltage sources should be replaced by short cicuit and all current sources should be replaced by an open circuit.
24 July 2017 at 12:12
your blog superb, you had published valuable information in #Short circuit Analysis. so we are providing more information about in Short circuit analysis is performed so that existing and new equipment ratings were sufficient to with stand the available short circuit current. This short circuit analysis can be done either through hand calculations or through known software like NEPLAN. if you want to know more information, please visit.. Short Circuit Analysis
3 April 2018 at 10:44
Great Blog,Thanks for sharing such beautiful information with us. I hope to will share some more information about Short Circuit Analysis. Please visit our website Short Circuit Analysis
24 May 2020 at 23:06
You wrote the wrong statement on superposition. In that all independent voltage sources are short circuited and current sources are open circuited instead you wrote it in opposite manner. Thank you.
Post a Comment