ECE

INDUCTOR

INDUCTOR

The inductor is a coil which stores energy in the magnetic field
Consider a wire of length l forming a loop of area A as shown on Figure 11. A current i(t) is flowing through the wire as indicated. This current generates a magnetic field B which is equal to

                                   
Where μ is the magnetic permeability of the material enclosed by the wire.
                          
The magnetic flux, Φ, through the loop of area A is
                            

Where we have defined 
                                       
From Maxwell’s equations we know that
                                  
And by taking L to be a constant we obtain the current-voltage relationship for this loop of wire also called an inductor.
                                   
The parameter L is called the inductance of the inductor. It has the unit of Henry (H).
The circuit symbol and associated electrical variables for the inductor is shown on Figure
                           
                                

For DC signals (di/dt=0) the inductor acts as a short circuit (v=0). Also note the inductor does not like current discontinuities since that would require that the voltage across it goes to infinity 


which is not physically possible. (We should keep this in mind when we design inductive devices. The current through the inductor must not be allowed to change instantaneously.)
If we integrate Equation (1.27) over time we have
                                      
The constant i(0) represents the current through the inductor at time t=0. (Note that we have also assumed that the current at t-->∞ was zero.)
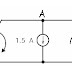
Let’s now consider the circuit shown on Figure where an inductor of inductance L is connected to a time varying current source i(t). 
                                         
If we assume that the current i(t) has the form
                                             
Then the voltage v(t) becomes
                                            
Therefore the current going through an inductor and the voltage across the inductor are 90 degrees out of phase. Here the voltage leads the current by 90 degrees.
The general plot of the voltage and current of an inductor is shown on Figure
         

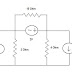
Inductor connected in series and in parallel combine to an equivalent inductance. Let’s first consider the parallel combination of inductors as shown on Figure 15. Note that all inductors have the same voltage across them.


By applying KCL we obtain
                            


                       Inductors in parallel combine like resistors in parallel


Next let’s look at the series combination of inductors as shown on Figure

Now by applying KVL around the loop we have
                     
                            Inductor in series combine like resistor in series

The energy stored in an inductor is the integral of the instantaneous power delivered to the inductor. Assuming that the inductor had no current flowing through it at then the energy stored in the inductor at time t is

                           

Real Inductors.

There are two contributions to the non-ideal behavior of inductors.
1. The finite resistance of the wire used to wind the coil
2. The cross turn effects which become important at high frequencies
The non-ideal inductor may thus be modeled as shown on Figure


In addition to the resistive non-idealities of inductors there could also be capacitive effects. These effects usually become important at high frequencies. Unless stated otherwise, these effects will be neglected in out analysis.

This post was written by: Author Name

Author description goes here. Author description goes here. Follow him on Twitter