Thursday, 14 February 2013
CAPACITOR
Do you like this story?
CAPACITOR
In both digital and analog electronic circuits a capacitor is a fundamental element. It enables the filtering of signals and it provides a fundamental memory element.
The capacitor is an element that stores energy in an electric field.
The circuit symbol and associated electrical variables for the capacitor is shown on Figure
The capacitor may be modeled as two conducting plates separated by a dielectric as shown on Figure .
When a voltage v is applied across the plates, a charge +q accumulates on one plate and a charge –q on the other.
If the plates have an area A and are separated by a distance d, the electric field generated across the plates is
and the voltage across the capacitor plates is
The current flowing into the capacitor is the rate of change of the charge across the capacitor plates And thus we have,
The constant of proportionality C is referred to as the capacitance of the capacitor. It is a function of the geometric characteristics of the capacitor - plate separation (d) and plate area (A) - and by the permittivity (ε) of the dielectric material between the plates.
Capacitance represents the efficiency of charge storage and it is measured in units of Farads (F).
The presence of time in the characteristic equation of the capacitor introduces new and exciting behavior of the circuits that contain them. Note that for DC (constant in time) signals (dv/dt= 0) the capacitor acts as an open circuit (i=0). Also note the capacitor does not like voltage discontinuities since that would require that the current goes to infinity which is not physically possible.
If we integrate Equation (1.5) over time we have
The constant of integration v(0) represents the voltage of the capacitor at time t=0.
The presence of the constant of integration v(0) is the reason for the memory properties of the capacitor.
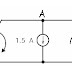
Let’s now consider the circuit shown on Figure where a capacitor of capacitance C is connected to a time varying voltage source v(t).
If the voltage v(t) has the form
Then the current i(t) becomes
Therefore the current going through a capacitor and the voltage across the capacitor are 90 degrees out of phase. It is said that the current leads the voltage by 90 degrees.
The general plot of the voltage and current of a capacitor is shown on Figure 4. The current leads the voltage by 90 degrees.
If we take the ratio of the peak voltage to the peak current we obtain the quantity Xc has the units of Volts/Amperes or Ohms and thus it represents some type of resistance. Note that as the frequency ω→0 the quantity Xc goes to infinity which implies that the capacitor resembles an open circuit .
Capacitors do like to pass current at low frequencies
As the frequency becomes very large ω→∞ the quantity Xc goes to zero which implies that the capacitor resembles a short circuit.
Capacitors like to pass current at high frequencies
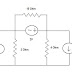
Capacitors connected in series and in parallel combine to an equivalent capacitance. Let’s first consider the parallel combination of capacitors as shown on Figure 5. Note that all capacitors have the same voltage, v, across them.
By applying KCL we obtain
Capacitors connected in parallel combine like resistors in series
Next let’s look at the series combination of capacitors as shown on Figure
Capacitors in series combine like resistors in parallel
By extension we can calculate the voltage division rule for capacitors connected in series. Here let’s consider the case of only two capacitors connected in series as shown on
The same current flows through both capacitors and so the voltages v1 and v2 across them are given by:1
And KVL around the loop results in
Which in turn gives the voltages v1 and v2 in terms of v and the capacitance:
Similarly in the parallel arrangement of capacitors the current division rule is
The instantaneous power delivered to a capacitor is
The energy stored in a capacitor is the integral of the instantaneous power. Assuming that the
capacitor had no charge across its plates at then the energy stored in the capacitor at time t is
Real Capacitors.
If the dielectric material between the plates of a capacitor has a finite resistivity – as compared to infinite resistivity in the case of an ideal capacitor – then there is going to be a small amount of current flowing between the capacitor plates. In addition there are lead resistance and plate effects.
In general the circuit model of a non-ideal capacitor is shown on Figure
The resistance Rp is typically very large and it represents the resistance of the dielectric material. Resistance Rs is typically small and it corresponds to the lead and plate resistance as well as resistance effects due to the operating conditions (for example signal frequency)
In practice we are concerned with the in series resistance of a capacitor called the Equivalent Series Resistance (ESR). ESR is a very important capacitor characteristic and must be taken into consideration in circuit design. Therefore the non-ideal capacitor model of interest to us is shown on
Typical values of ESR are in the mΩ-Ω range.

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter


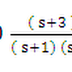





0 Responses to “CAPACITOR”
Post a Comment