Monday, 11 March 2013
MAXIMUM POWER TRANSFER
Do you like this story?
Maximum power transfer theorem
A load will receive maximum power from a linear bilateral dc
network when its total resistive value is exactly equal to the Thévenin resistance
of the network as “seen” by the load.
Different cases in Maximum power transfer theorem
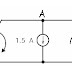
1) source resistance and variable load
I = VS / ( RS + RL )
Power ( p) = I2 RL = VS2
RL / (RS + RL)2
For maximum power differentiate power with load resistance
and equate it with zero
VS2 [ (RS+RL)2
– RL (2(RS + RL)] = 0
RS2+RL2+2 *RS*RL
-2 *RS*RL – 2RL2 =0
RS2 - RL2 = 0
RS = RL
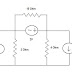
2) Source impedance and variable load impedance
I = VS / (RS+RL+j(XS+XL))
Taking magnitude of current
I = VS / √ [(RS+RL)2+(XS+XL)2]
P = | I |2 RL
P = VS2 RL/ [(RS+RL)2+(XS+XL)2]
a) Variable RL
For maximum power differentiate power with load resistance (
RL ) and equate it with zero
dp = VS2
[(RS+RL)2+(XS+XL)2]-
2(RS+RL)RL = 0
dRL [(RS+RL)2+(XS+XL)2] 2
dRL [(RS+RL)2+(XS+XL)2] 2
[(RS+RL)2+(XS+XL)2]-
2(RS+RL)RL
= 0
RS2+RL2+2
*RS*RL -2 *RS*RL – 2RL2
+(XS+XL)2 = 0
RS2
- RL2+(XS+XL)2 = 0
RL = √[
RS2 +(XS+XL)2]
b) Variable XL
For maximum power differentiate power with load impedance (
XL ) and equate it with zero
dp = VS2
[(RS+RL)2+(XS+XL)2]*0
- 2(XS+XL)RL = 0
dXL [(RS+RL)2+(XS+XL)2] 2
dXL [(RS+RL)2+(XS+XL)2] 2
VS2 [(RS+RL)2+(XS+XL)2]*0
- 2(XS+XL)RL = 0
XS+XL = 0
c) Both RL and XL are variable
this case is a combination of cases a nad b
RL = √[ RS2
+(XS+XL)2]
----------1
XS+XL = 0
XS = -XL ----------------------------2
Substituting 2 in 1 we get
RL = RS
ZL = RL + j XS
= RL
– j XL
ZL = ZS*
3) ZS and variable load resistance
For this maximum power transfer when
RL = | ZS
|

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter
Subscribe to:
Post Comments (Atom)











2 Responses to “MAXIMUM POWER TRANSFER”
13 March 2013 at 22:24
nice blog. !!!
5 December 2013 at 05:03
Very helpful blog ...thanks a lott !!!
Post a Comment