Tuesday, 19 March 2013
DUAL SLOPE INTEGRATING TYPE DVM
Do you like this story?
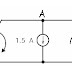
Switch
connected to +VM
Once
VM is connected, the capacitor starts charging linearly then the
output at the integrator decreases linearly. This linearly decreasing ramp is
fed to inverting terminal of the zero crossing detector. Since the input at non
inverting terminal is greater than inverting terminal, it produces a positive
going pulse. This positive going pulse makes the gating circuit to start. Now pulses
produced by the clock generator passess through gating circuit and counter
count the number of pulses.
t
VC
= 1/C ∫ I dt
-∞
t1
= 1/C ∫ VM / R dt
0
=
VM
/ RC ( t1 – 0 )
= VMt1/RC
=
VMT1/RC (t1 =T1)
V0
= -VC
V0
= - ( VMT1/RC )
Let
T1 be the time taken by the capacitor to charge to VM
ie.,from 0 to t1
let
NF be the number of pulses counted during T1
T1=
NF tCLK (tCLK = clock period of pulses produced
by the clock generator)
When
the counter reaches maximum state a reset pulse is produced by the counter
which automatically changes the switch from +VM to - VREF
Switch
connected to –VREF
Once
VREF is connected, the capacitor starts discharging linearly then
the output at the integrator increases linearly. The output of ZCD is still positive,
hence gating circuit is on. So the counter still counts the pulses. When
voltage reaches t2 and crosses zero the input to the inverting
terminal of ZCD is greater than input to the non inverting terminal the output of
ZCD is a negative going pulse, which makes the gating circuit to switch off. At
t2 the capacitor completely discharges.
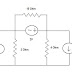
Graphs
of VC and V0
Let
T2 = t2-t1 be the time taken by the capacitor
to discharge completely to zero
Let
n be the number of clock pulses during T2
T2
= n tCLK
t2
VC
= 1/C ∫ I dt + initial voltage
t1
t2
= 1/C ∫ -VREF / R dt + VMT1/RC
t1
= - VREF / RC ( t2 – t1
) + VMT1/RC
=-
VREF / RC ( T2 ) + VMT1/RC ( t2 – t1 = T2 )
V0
= -VC
V0
= VREF / RC ( T2 ) - VMT1/RC
At
t2 ,V0 =0
VREF
/ RC ( T2 ) - VMT1/RC =0
VREF / RC ( T2 ) = VMT1/RC
Substituting
the values of T1= NFtCLK and T2= n
tCLK we get
VM
= (n VREF )/ NF
Features
1)
Conversion time
tCONV = T1 + T2
= NFtCLK + n
tCLK
Since
Conversion time of this DVM is long and variable its speed is less
2)
Noise rejection
As
we are integrating voltage for time duration we are calculating true average value.
So if an AC signal or noise is super imposed on VM,it will be averaged.
Hence effect of noise is less. Therefore noise rejection is high.
3)
Accuracy
As
VM doesn’t depends on R and C accuracy is more

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter
Subscribe to:
Post Comments (Atom)









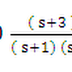






0 Responses to “DUAL SLOPE INTEGRATING TYPE DVM”
Post a Comment