Thursday, 25 April 2013
TRANSISTOR PROBLEM 6
Do you like this story?
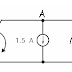
Consider
VBE1 = VBE2 = 0.7 V,β1 = 100,β2=50.
Find IB1,IB2,I1,I2,IC2,IE1,V01,V02
SOLUTION
By applying thevenin’s theorem at
input
VTH = VCC R2
/ (R1 + R2 )
= 24*10 / (10 + 82)
= 2.61V
RTH = 82 || 10 = 8.91 KΩ
Applying KVL at the input
12 – (8.91 KΩ + 100 KΩ )IB2
– VBE2 – VBE1 – (IE1 * 100Ω )= 0
IE2= ( β2 + 1 )IB2
= 51 IB2
IB1 = IE2
IE1 = ( β1 + 1 )
IB1 = ( β1 + 1 ) ( β2 + 1 )IB2 =101
* 51 * IB2
= 5151 * IB2
= 5151 * IB2
2.61 – ( 108.91 KΩ * IB2 )
– 0.7 – 0.7 – ( 5151 * IB2 * 100Ω ) = 0
620.1K* IB2 = 1.21
IB2 = 1.21 / 624.01K
= 1.94 µA
= 9.98 mA
IE2 = 51 * IB2
= 98.94 µA
IB1 = IE2 = 98.94
µA
IC1 = β1 * IB1
= 100 * 98.94 µA
=9.894 mA
IC1 =( 24 – V01 )/ 1K
9.894 mA = ( 24 – V01 )/ 1K
V01 = 24 - 9.894
= 14.11 V
V02 = IE1 * 100
= 9.98 mA * 100
= 0.998 V
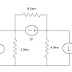
Applying KVL
10 KΩ*I2 – 100*IB2
- 0.7 - 0.7 - V02 = 0
10 KΩ*I2 – 100*1.94 µA
- 0.7 - 0.7 – 0.998 = 0
I2 = 0.2593 mA
I1 = IB2 + I2
= 1.94µA +0.2593mA
= 0.261 mA

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter
Subscribe to:
Post Comments (Atom)











0 Responses to “TRANSISTOR PROBLEM 6”
Post a Comment