Saturday, 25 May 2013
WAVE POLARIZATION
Do you like this story?
Consider a wave propagating in Z direction. So the
components present are EX,EY,HX,HY
and the components EZ = HZ = 0
Polarization is not present in the direction of wave
propagation
Consider E = E1 cos (ωt-βz )aX +
E2 cos (ωt-βz+φ )aY
The wave is propagating is in positive Z direction
Where φ indicates phase difference between x and y
components of the field.
If φ = 0 then the wave is linearly polarized
If φ = 90, E1 = E2, then the wave
is circularly polarized
If φ = 90, E1 ≠ E2, then the wave
is elliptically polarized
If φ = some phase difference, E1 ≠ E2,
then the wave is elliptically polarized with an inclination equal to phase
difference
Example 1
E = sin (ωt-βz )aX + sin (ωt-βz+900
)aY
Solution
As there is a phase difference of 90 and E1
= E2, we can say it is circularly polarized
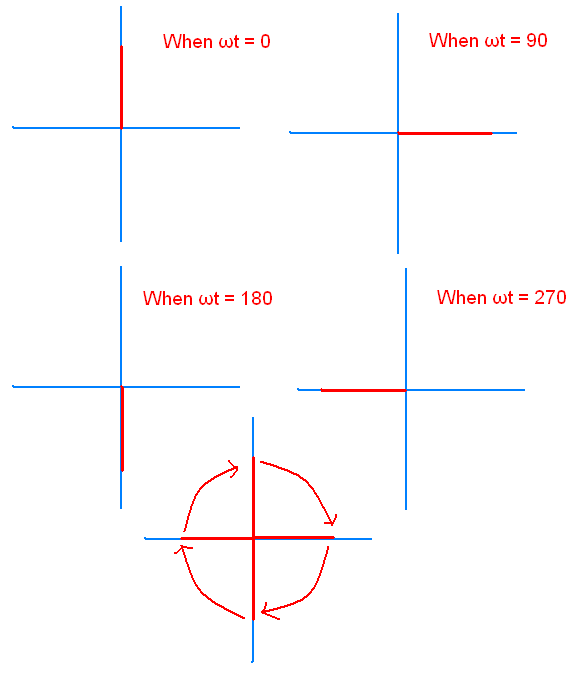
How to identify whether it is left or right handed.
First fix the orientation point by keeping propagation
direction = 0 ie., Z= 0
Now substitute ωt =0,90,180,270,360
When ωt = 0
E = aY
When ωt = 90
E = aX
When ωt = 180
E = - aY
When ωt = 270
E = - aX
Now
point your thumb finger in the direction of propagation and close your fingers
according to the components appear on the graph, which hand suits the closing
fingers with the direction of propagation gives left hand or right hand.
Positive Z direction upwards, negative Z direction
downwards.
For the obtained graph left hand suits. So it is left
circularly polarized.
Example 2
E = ( aX + 2 ej(∏/2) aY)
ej(ωt+βz )
Solution
Expand ejθ = cos θ + jsinθ
E =( aX + 2 ( cos 90 + jsin 90 ) aY)
*( cos (ωt+βz ) + j sin ( ωt+βz )
E =( aX + 2 j aY) *( cos (ωt+βz )
+ j sin ( ωt+βz )
Know take real part of E
E = ( cos (ωt+βz ) aX – 2 sin ( ωt+βz ) aY
Comparing with general expression of E
We can say that wave is going in negative Z direction
First fix the orientation point by keeping propagation
direction = 0 ie., Z= 0
Now substitute ωt =0,90,180,270,360
When ωt = 0
E = aY
When ωt = 90
E = -2 aX
When ωt = 180
E = - aY
When ωt = 270
E = + 2 aX
Draw the graph as above example
For the obtained graph left hand suits. So it is left
elliptically polarized.
Example 3
E = sin (ωt+βx)( aY + jaZ)
Solution
E = sin (ωt+βx) aY + sin (ωt+βx + 90)aZ
We can say that wave is going in negative X direction
When ωt = 0
E = aZ
When ωt = 90
E = aY
When ωt = 180
E = - aZ
When ωt = 270
E = - aY
Draw the graph as above example
For the obtained graph left hand suits. So it is right
circularly polarized.

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter
Subscribe to:
Post Comments (Atom)







0 Responses to “WAVE POLARIZATION”
Post a Comment