Wednesday, 8 May 2013
P,D,I CONTROLLERS
Do you like this story?
A controller is a device which is used to control
transient and steady state response as per the requirement.
A good system demands less rise time, less settling
time, small peak overshoot and less steady state error.
PROPORTIONAL
CONTROLLER
Proportional controller cannot eliminate error
completely.
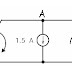
Example:
From above transfer function ωn =
1
2ξ ωn =
5
ξ = 2.5 > 1
Therefore
the system is over damped
After proportional controller Kp
ωn =
Kp
2ξ ωn =
5
ξ = 2.5 / Kp
So, damping factor depends on Kp
By proper selection of Kp we required
response
If Kp increases then ξ decreases.
As ξ
decreases the peak over shoot increases so that the system becomes less stable.
INTEGRAL
CONTROLLER
It decreases steady state error but the system becomes
less stable
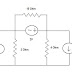
Example:
Characteristic equation is S2 + 5S + 1
Transfer function of integral controller = KI /
S
The integral controller adds one pole at origin which
increases the TYPE of the system. As the TYPE increases the steady state error
decreases, but the system stability decreases.
By applying controller
Characteristic equation is S3 + 5S2
+ KI =0
According to RH criteria all powers should be present
in the characteristic equation. In the above equation ‘S’ is missing. Therefore
the system becomes unstable.
DERIVATIVE
CONTROLLER
It improves system stability but steady state error
increases
Example:
Characteristic equation is S3 + 5S2
+ 1
Transfer function of derivative controller = KD S
The derivative controller adds one zero at origin which
decreases the TYPE of the system. As TYPE decreases system becomes stable.
If TYPE decreases steady state error increases
Applying derivative controller
Characteristic equation is S2 + 5S + KD
By comparing the characteristic equation we can infer
that system becomes stable

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter
Subscribe to:
Post Comments (Atom)


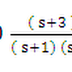





0 Responses to “P,D,I CONTROLLERS”
Post a Comment