Friday, 10 May 2013
PI CONTROLLER
Do you like this story?
It decreases the steady state error without effecting
the stability
Its transfer function is KP + KI
/ S = (KPS + KI)/S
PI controller adds one pole at origin which increases TYPE.
As TYPE increases steady state error decreases.
It also adds one finite zero in left of s-plane which
avoids the effect on stability
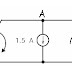
Example
Characteristic equation is S2 + 5S + 1=0
Applying controller
TYPE increases. So steady state error decreases
Characteristic equation S3 + 5S2
+ KPS+ KI = 0
All powers of S are there in above equation. So no
effect o stability
EFFECT ON DAMPING FACTOR
Characteristic equation is S2 + 5S + 1 =0
From the above characteristic equation
ξ=
2.5
After applying controller (S+ 5)/S
G(S) H(S) = 1/S2
Characteristic equation is S2 + 1 =0
ξ= 0
We can infer that there is a decrement in the value
ξ
As ξ decreases peak over shoot increases
From above calculations
1) Damping factor decreases.
2) Peak over shoot increases.
3) Rise time decreases.( To verify this substitute two
different values of ξ in Tr formula )
4) Bandwidth increases, since Tr is
inversely proportion to bandwidth.
5) Settling increases as it is inversely proportional
to ξ.( To verify this substitute two different values of ξ in Ts
formula )
6) Affect on gain margin and phase margin
GAIN
MARGIN
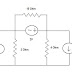
Example
Without controller
Solution
For ωpc
-180 = -90 – tan-1(ω)- tan-1(ω/2)
By solving above equation we get
ωpc =
√2 rad/sec
Gain margin = -20 log | G(s) H(s) | at ωpc
| G(s) H(s) | at ωpc = 1/6
Gain margin= 15.5 db
For simplicity for calculation I assume controller (s +
1)/s
For ωpc
-180 = -180 – tan-1(ω) - tan-1(ω/2)
+ tan-1(ω)
ωpc = 0
| G(s) H(s) | at ωpc = ∞
Gain margin= -∞
So,
We Can Infer That There Is A Decrease In Gain Margin
PHASE
MARGIN
Without controller
Solution
For ωgc
| G(s) H(s) | at ωgc = 1
ω4+2ω2-1 =0
finding roots we get ωgc = 0.6435
PM = 180 + angle (G(s) H(s) | at ωgc
= 180 -90 -
tan-1(ω/2)
= 90- tan-1(0.6435/2)
= 72.16
For simplicity for calculation I assume controller (s +
2)/s
For ωgc
| G(s) H(s) | at ωgc = 1
1/ω2
= 1
ω2 = 1
finding roots we get ωgc = 1
PM = 180 + angle (G(s) H(s))| at ωgc
= 180 -180
= 0
From
Above Two PM’s we can conclude that PM decreases

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter
Subscribe to:
Post Comments (Atom)









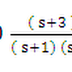





0 Responses to “PI CONTROLLER”
Post a Comment