Saturday, 4 May 2013
DOMINANT POLE
Do you like this story?
The poles of a system (those closest to the imaginary axis in the
s-plane) give rise to the longest lasting terms in the transient response of
the system.Then those poles are called dominant poles
The poles which are far from imaginary axis are called insignificant
poles because their their exponential terms decay very fast.
If we find inverse Laplace transform to a transfer function,
in the response we get exponential terms with powers in terms of poles, not
with zeros. So we have only dominant poles and we won’t have dominant zeros.
y(t) = (2 − 2.222e-t + 0.2469e−10t − 0.0022e−100t)u(t)
Note that
The first term
(2) is the forced response. It remains as long as the input remains equal to 1.
The second term
(-2.22e-t) has an initial condition 9x larger than any other term and it decays
slower than the other terms.
The steady state
response is when t = -∞
Substitute the
some value t in y ( t ).you can clearly notice which term is affecting the
steady state value. The terms which are affecting more is called dominant.
Hence, the pole at s=-1 dominates the response (and is termed the dominant
pole).
Dominant pole approximation
Solution
Select the pole which is near to jω axis
So, dominant pole is -1.This controls the system
response
Know divide other poles with the dominant pole. Generally
If the value when divided by other poles with the dominant pole is greater than 5, then that pole is subjected to dominant pole
approximation.
So from the given transfer function poles at -6, -7 are
subjected to dominant pole approximation
How to apply subjected to dominant pole approximation
Take the values that are subjected to dominant pole
approximation as common from those expressions in which the values that are
subjected to dominant pole approximation are present. Then substitute S = 0 in
the expressions in which the values that are subjected to dominant pole
approximation are present.
Solution
The dominant conjugate poles are -(1+j2),-(1−j2)

This post was written by: Author Name
Author description goes here. Author description goes here. Follow him on Twitter
Subscribe to:
Post Comments (Atom)



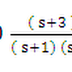





5 Responses to “DOMINANT POLE”
13 January 2015 at 23:15
nicely explained!!
17 December 2015 at 02:03
Clear concept is generated by watching this.
23 November 2017 at 02:04
Exactly
28 June 2018 at 10:21
clear explanation thank you
16 November 2018 at 14:01
Very well explained...
Post a Comment