Friday, 21 June 2013
In a broad cast super
hetero dyne receiver having no RF amplifier, the load Q of the antenna coupling
circuit is 100. If the IF frequency is 455 KHz, determine
A) The image frequency and
its rejection ratio for tuning at 1.1 KHz station.
B) The image frequency and
its rejection ratio for tuning at 25 MHz station.
Solution
Given IF frequency is 455 KHz
Quality factor Q = 100
a) fS
= 1.1 KHz
Image
frequency fSi = fS
+ 2 fi
= 1100 +( 2 * 455 )
= 2010 KHz
ρ = (fSi/fS)
– (fS/fSi)
= (2010/1100) – (1100/2010)
=1.28
Image rejection ratio
α = √( 1+ Q2 ρ2 )
= √( 1+ 1002 1.282 )
= 128
b) fS
= 25 MHz
Image
frequency fSi = fS
+ 2 fi
= 25 MHz +( 2 * 455 )
= 25.91 MHz
ρ = (fSi/fS)
– (fS/fSi)
= (25.91 /25) – (25/25.91)
= 0.0715
Image rejection ratio
α = √( 1+ Q2 ρ2 )
= √( 1+ 1002 0.07152 )
= 5.22
Thus rejection is poor for
practical receiver in HF band
So, we can say that it is
not a major problem for standard AM receiver without an RF stage, but it causes
problem at high frequencies using same intermediate frequency.
We can eliminate this
problem by introducing RF stage or by increasing intermediate frequency
Friday, 21 June 2013 by Unknown · 0
Thursday, 20 June 2013
RF
SECTION
The signal from
the antenna is tuned and may be amplified in a so-called radio frequency (RF)
amplifier, although this stage is often omitted. One or more tuned circuits at
this stage block frequencies which are far removed from the intended reception
frequency. In order to tune the receiver to a particular station, the frequency
of the local oscillator is controlled by the tuning knob (for instance). Tuning
of the local oscillator and the RF stage may use a variable capacitor, or
varicap diode. The tuning of one (or more) tuned circuits in the RF stage must
track the tuning of the local oscillator.
MIXER/CONVERTER
SECTION
The signal is
then fed into a circuit where it is mixed with a sine wave from a variable
frequency oscillator known as the local oscillator (LO). The mixer uses a
non-linear component to produce both sum and difference beat frequencies
signals, each one containing the modulation contained in the desired signal.
The output of the mixer may include the original RF signal at fd,
the local oscillator signal at fLO, and the two new frequencies fd+fLO
and fd-fLO. The mixer may inadvertently produce
additional frequencies such as 3rd- and higher-order inter-modulation products.
The undesired signals are removed by the IF band pass filter, leaving only the
desired offset IF signal at fIF which contains the original
modulation (transmitted information) as the received radio signal had at fd.
INTERMEDIATES
FREQUENCY AMPLIFIER
Like the RF amplifier,
the IF amplifier must effectively amplify the incoming signal. In the case of
Intermediate Frequencies, amplification and filtering are often utilized
simultaneously. It is also not uncommon for several stages of IF amplifiers to
used in succession. The amplified IF output then proceeds to Limiter, Automatic
Gain Control, and Discriminator circuitry.
WHY
IF IS USED
Intermediate
frequencies are used for three general reasons. At very high (gigahertz)
frequencies, signal processing circuitry performs poorly. Active devices such
as transistors cannot deliver much amplification (gain) Ordinary circuits using
capacitors and inductors must be replaced with cumbersome high frequency
techniques such as strip lines and waveguides. So a high frequency signal is
converted to a lower IF for more convenient processing. For example, in
satellite television receivers, converting the microwave down-link signal to a
much lower intermediate frequency at the dish allows a relatively inexpensive
coaxial cable to carry the signal to the rest of the receiver inside the
building.
A second reason,
in receivers that can be tuned to different frequencies, is to convert the
various different frequencies of the stations to a common frequency for
processing. It is difficult to build amplifiers, filters, and detectors that
can be tuned to different frequencies, but easy to build tunable oscillators.
Super hetero dyne receivers tune in different frequencies by adjusting the
frequency of the local oscillator on the input stage, and all processing after
that is done at the same fixed frequency, the IF. Without using an IF, all the
complicated filters and detectors in a radio or television would have to be
tuned in unison each time the frequency was changed, as was necessary in the early
tuned radio frequency receivers.
The main reason
for using an intermediate frequency is to improve frequency selectivity. In
communication circuits, a very common task is to separate out or extract
signals or components of a signal that are close together in frequency. This is
called filtering. Some examples are, picking up a radio station among several
that are close in frequency, or extracting the chrominance sub carrier from a
TV signal. With all known filtering techniques the filter's bandwidth increases
proportionately with the frequency. So a narrower bandwidth and more
selectivity can be achieved by converting the signal to a lower IF and
performing the filtering at that frequency.
DETECTOR/DEMODULATOR
SECTION
The received
signal is now processed by the demodulator stage where the audio signal (or
other baseband signal) is recovered and then further amplified. AM demodulation
requires the simple rectification of the RF signal (so-called envelope
detection), and a simple RC low pass filter to remove remnants of the
intermediate frequency.FM signals may be detected using a discriminator, ratio
detector, or phase-locked loop. CW (Morse code) and single sideband signals
require a product detector using a so-called beat frequency oscillator, and there
are other techniques used for different types of modulation. The resulting
audio signal (for instance) is then amplified and drives a loudspeaker.
When so-called
high-side injection has been used, where the local oscillator is at a higher
frequency than the received signal (as is common), then the frequency spectrum
of the original signal will be reversed. This must be taken into account by the
demodulator (and in the IF filtering) in the case of certain types of
modulation such as single sideband.
COMMONLY
USED INTERMEDIATE FREQUENCIES
1)110 kHz was
used in Long wave broadcast receivers
2) Analogue
television receivers using system M: 41.25 MHz (audio) and 45.75 MHz (video).
Note, the channel is flipped over in the conversion process in an inter carrier
system, so the audio IF frequency is lower than the video IF frequency. Also,
there is no audio local oscillator; the injected video carrier serves that
purpose.
3) Analogue
television receivers using system B and similar systems: 33.4 MHz. for aural
and 38.9 MHz. for visual signal.(The discussion about the frequency conversion
is the same as in system M)
4) FM radio
receivers: 262 kHz, 455 kHz, 1.6 MHz, 5.5 MHz, 10.7 MHz, 10.8 MHz, 11.2 MHz,
11.7 MHz, 11.8 MHz, 21.4 MHz, 75 MHz and 98 MHz. In double-conversion super
hetero dyne receivers, a first intermediate frequency of 10.7 MHz is often
used, followed by a second intermediate frequency of 470 kHz. There are triple
conversion designs used in police scanner receivers, high-end communications
receivers, and many point-to-point microwave systems.
5)AM radio
receivers: 450 kHz, 455 kHz, 460 kHz, 465 kHz, 470 kHz, 475 kHz, 480 kHz
6) Satellite
unlink-downlink equipment: 70 MHz, 950-1450 Downlink first IF
7) Terrestrial
microwave equipment: 250 MHz, 70 MHz or 75 MHz
8) Radar: 30 MHz
Thursday, 20 June 2013 by Unknown · 0
Saturday, 25 May 2013
Consider a wave propagating in Z direction. So the
components present are EX,EY,HX,HY
and the components EZ = HZ = 0
Polarization is not present in the direction of wave
propagation
Consider E = E1 cos (ωt-βz )aX +
E2 cos (ωt-βz+φ )aY
The wave is propagating is in positive Z direction
Where φ indicates phase difference between x and y
components of the field.
If φ = 0 then the wave is linearly polarized
If φ = 90, E1 = E2, then the wave
is circularly polarized
If φ = 90, E1 ≠ E2, then the wave
is elliptically polarized
If φ = some phase difference, E1 ≠ E2,
then the wave is elliptically polarized with an inclination equal to phase
difference
Example 1
E = sin (ωt-βz )aX + sin (ωt-βz+900
)aY
Solution
As there is a phase difference of 90 and E1
= E2, we can say it is circularly polarized
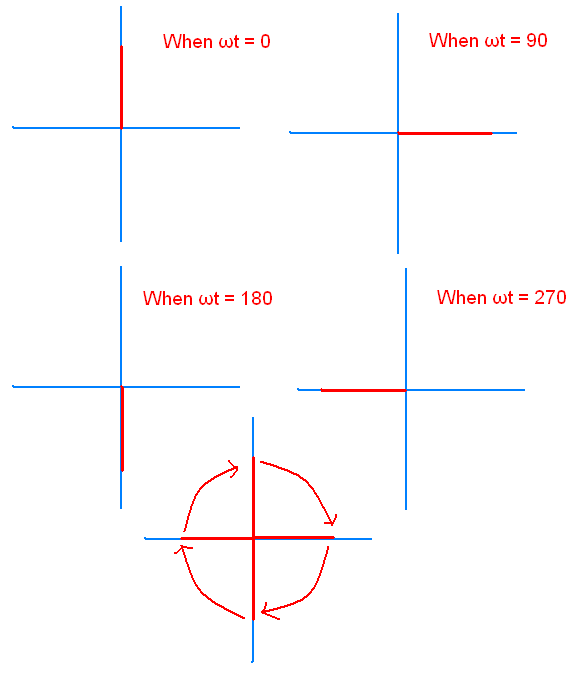
How to identify whether it is left or right handed.
First fix the orientation point by keeping propagation
direction = 0 ie., Z= 0
Now substitute ωt =0,90,180,270,360
When ωt = 0
E = aY
When ωt = 90
E = aX
When ωt = 180
E = - aY
When ωt = 270
E = - aX
Now
point your thumb finger in the direction of propagation and close your fingers
according to the components appear on the graph, which hand suits the closing
fingers with the direction of propagation gives left hand or right hand.
Positive Z direction upwards, negative Z direction
downwards.
For the obtained graph left hand suits. So it is left
circularly polarized.
Example 2
E = ( aX + 2 ej(∏/2) aY)
ej(ωt+βz )
Solution
Expand ejθ = cos θ + jsinθ
E =( aX + 2 ( cos 90 + jsin 90 ) aY)
*( cos (ωt+βz ) + j sin ( ωt+βz )
E =( aX + 2 j aY) *( cos (ωt+βz )
+ j sin ( ωt+βz )
Know take real part of E
E = ( cos (ωt+βz ) aX – 2 sin ( ωt+βz ) aY
Comparing with general expression of E
We can say that wave is going in negative Z direction
First fix the orientation point by keeping propagation
direction = 0 ie., Z= 0
Now substitute ωt =0,90,180,270,360
When ωt = 0
E = aY
When ωt = 90
E = -2 aX
When ωt = 180
E = - aY
When ωt = 270
E = + 2 aX
Draw the graph as above example
For the obtained graph left hand suits. So it is left
elliptically polarized.
Example 3
E = sin (ωt+βx)( aY + jaZ)
Solution
E = sin (ωt+βx) aY + sin (ωt+βx + 90)aZ
We can say that wave is going in negative X direction
When ωt = 0
E = aZ
When ωt = 90
E = aY
When ωt = 180
E = - aZ
When ωt = 270
E = - aY
Draw the graph as above example
For the obtained graph left hand suits. So it is right
circularly polarized.
Saturday, 25 May 2013 by Unknown · 0
Subscribe to:
Comments (Atom)